Amplitude-Biased And Amplitude-Unbiased Cross-Correlations:

An Illustration With Three Examples

Martin Schimmel

General Motivation:

An important problem in seismology is the unambiguous detection of seismic arrivals to constrain the corresponding Earth structure. Often, difficulties arise because of the variability and abundance of signals in the seismograms. The large amplitude signals are mostly caused by the gross structure of the Earth and although these signals vary in shape, they can be detected due to their outstanding amplitudes. Weak signals, however, are mostly concealed in other signals with similar amplitudes. As a consequence, the weak signals can only be detected because of their coherent appearance on different seismograms or their resemblance with a given reference or pilot wavelet such as the direct P arrival or the imposed ground signal of a vibrating source. The detection, arrival time picking and/or extraction of weak signals require therefore the use of coherence measures. Since the weak signals are more sensitive to waveform perturbations than the large amplitude signals the problem consists in the detection of closely similar waveforms rather than completely coherent waveforms. To cope with this problem a variety of coherence measures have been innovated to evaluate quantitatively the goodness of fit obtained. These measures are mostly based on cross-correlation and stacking techniques which are used widely at various stages of data processing. To enable the detection of weak signals concealed in other larger amplitude signals by waveform semblance the coherence measures should be amplitude unbiased.
 

Cross-Correlations:

The cross-correlation (CC) between two data sets measures their similarity as a function of time shift or time lag. This measure involves the progressively sliding of one waveform past the other and summing the cross-multiplication products over the common time interval of the waveforms. The cross-correlation function will be peaked at time lags when the (closely) similar waveforms are best aligned. Dissimilar waveforms cause the cross-correlation function to have small amplitudes due to the summation of positive and negative cross-multiplication products.

In our paper ( abstract) we extend the concept of the phase stack (Schimmel and Paulssen, 1997)and present a new cross-correlation function which we call phase cross-correlation (PCC). The proposed function can be used as coherence functional, for signal recognition, and arrival time picking. We show synthetic applications which are discussed in comparison with the conventional cross-correlation (CC) and the geometric normalized cross-correlation (CCGN). It is shown that the geometric normalized cross-correlations and phase cross-correlations of closely similar waveforms can lead to different results due to their different design philosophies. The geometrical normalized cross-correlation is insensitive to the amplitude changes between data sets but is biased by the large amplitude portions within the considered correlation windows. Conversely, PCC equally weights every sample in the correlation and is consequently insensitive to the amplitudes within the correlation windows.

In the following we show some examples to illustrate the effect of amplitude biased and unbiased correlations. For more details and figures see the paper by Schimmel (1999). In Schimmel et al. (2011) you can find other examples and comparisons. The goal of this last paper is to show how PCC can improve the seismic ambient noise signal (empirical Green's function) extraction. PCC has also been implemented in the multi-channel cross-correlation approach of VanDecar and Crosson (1990) to compute the cross-correlations between all possible pairs of traces to estimate relative phase arrival times in a LSQ fashion for travel time tomography (Schimmel et al., 2003).
 

Example 1:

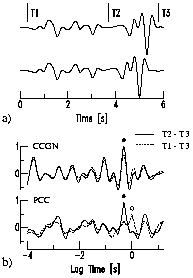a) Waveforms used for cross-correlations. Both traces consist of the same two wave trains (T1-T2 and T2-T3). The last wave train has been shifted by -0.2 s on the bottom trace. The top trace is used to extract two different pilots (T2 to T3 and T1 to T3) which are cross-correlated with the bottom trace. b) Cross-correlograms (top: CCGN, bottom: PCC) for the pilots T2-T3 (solid line) and T1-T3 (dashed line).
 

The different determination of waveform similarity and the importance of the choice of the correlation window are combined in the first example. Figure a shows two traces which consist of two different wave trains each. The only difference between both traces is that the last wave train (T2-T3) of the second trace is shifted by -0.2 s. Two pilots have been extracted from the top trace using the windows T2 to T3 and T1 to T3 for correlation with the bottom trace. The resulting CCGN's and PCC's are shown in Figure b. The solid and dashed line style are used to distinguish the applied pilots from T2-T3 and T1-T3. As can be seen from Figure b, CCGN is hardly affected by the choice of the pilot. The best correlations which are marked with a black dot are obtained for a lag time of -0.2 s, i.e. by shifting the pilot until its second wave train matches with the second wave train of the second trace. Conversely, with the PCC-measure we obtain maximum correlation at 0 s and -0.2 s for the pilot from T1 to T3 and T2 to T3, respectively. This is due to the fact that PCC is amplitude insensitive and consequently determines its best coherence by the maximum number of coherent samples. In other words the zero lag alignment (dashed line) has been favored since it aligns the longest coherent wave train (T1-T2) within the pilot trace. The corresponding CCGN-measure does not favor a zero lag alignment since the large amplitude wave train (T2-T3) dominates the correlation. The small amplitude parts of the correlation window lead, even in the case of coherence, to small amplitude contributions which do not much affect the total correlation. This explains the large resemblance of both CCGN functions. The smaller absolute maxima of the dashed lines indicate the decreased similarity of the cross-correlated waveforms.
 

Example 2:
 

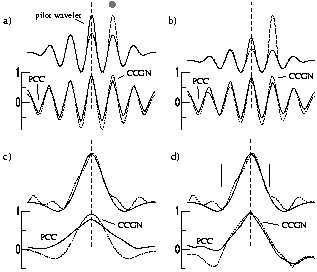a) Top: Pilot wavelet (solid line) in its full length and trace with distorted waveform (dashed line). The distorted waveform has zero amplitudes outside the time window shown. Bottom: PCC (solid line) and CCGN (dashed line) between the pilot and the distorted signal. Zero lag is marked by the vertical dashed line and corresponds to the relative position of the waveforms at the top. b) - d) show the same as a) for different waveforms. In d) the pilot decreased to the time window marked by the vertical lines.

The different sensitivities of the coherence measures to waveform similarity causes differences in the PCC and CCGN for waveforms which are not perfectly coherent. These differences are shown in the Figure. The traces at the top of each figure show the pilot wavelet (solid line) and the corresponding trace with the  closely similar waveform (dashed line). The pilot wavelet is shown in its full length while the other trace is continued with zero amplitudes outside the time window shown. The cross-correlations are plotted at the bottom of each figure. Zero lag is marked by the vertical dashed line. The lag time corresponds to a shift of the pilot wavelet relative to the other waveform.

 Figures a,b demonstrate that large amplitudes within the correlation window strongly influence the CCGN-measure. The CCGN from Figure a does not permit to decide whether the waveforms are best aligned at zero time lag or for a positive time lag which aligns the waveforms by their absolute maxima or absolute maximum and minimum. In other words, following this measure the pilot and the trace can be aligned in three different manners. The time lag for the alignment of the absolute maxima is marked with a grey dot. Conversely, from the PCC it is obvious that the best coherence is obtained at zero time lag only. The differences between the PCC- and the CCGN-measure are caused by their different concepts. The CCGN measure is based on the sum of cross-multiplication products which is strongest influenced by the largest amplitudes in the wavelets. To show this we further increased the absolute maximum of the dashed waveform from Figure a; the waveforms and corresponding correlograms are shown in Figure b.

As can be seen from this figure, the CCGN now favors the alignment of the waveforms by their absolute maxima. Conversely, PCC still advocates the alignment at zero lag. The PCC value at zero lag, however, decreases which means that the waveforms become less coherent by the modification.

The strong sensitivity of the CCGN to the large amplitudes in the waveforms has also an advantage. For instance, low amplitude noise within the correlation window will have its strongest impact when PCC is used. We show an example in Figures c and d. The PCC-measure is equally sensitive to all perturbations in the wavelet. As consequence, the coherence value at zero lag is smaller than for the CCGN (Figure c). In such a situation the chosen length of the time window of the pilot wavelet becomes important. In Figure d we demonstrate the results for a decreased time window. The begin and end times of the pilot wavelet are marked by the vertical bars. The PCC measure improves while the CCGN is little affected by this modification. Further, the Figure shows that the PCC maxima are more peaked than the maxima of the CCGN-measure. This and the importance of the choice of the correlation window support that PCC is more sensitive to waveform coherence. In other words, PCC permits to discriminate between closely similar waveforms. This is an advantage for travel time picking or the computation of objective functions.
 

Example 3:

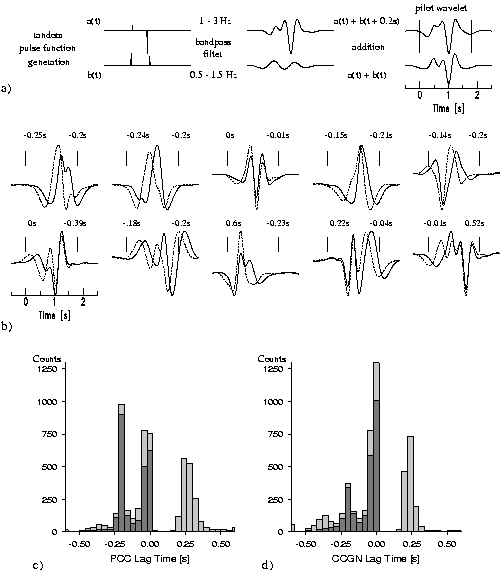
a) The sketch outlines the generation of closely similar waveform pairs by the addition of two randomly generated signals. The pilot wavelet is generated by shifting the low frequency signal by 0.2 s prior addition. b) 10 examples of randomly generated waveform pairs. The vertical bars mark the 1.8 s window of the pilot (solid line). The numbers at the upper left and right are the lag times of the best CCGN and PCC waveform fits. c) and d) The histograms show the lag time distributions of the best PCC and CCGN waveform fits of 5000 randomly generated waveform pairs. The dark grey area shows the distributions for the 2500 best correlations.

An example for a deterministic waveform perturbation is shown in the Figure. In Figure a we picture the procedure used to generate the closely similar waveform pairs. Two pulse functions are generated with two random amplitude spikes at random time within a 1 s window. The first and second pulse function have been band-passed at 1 - 3 Hz and 0.5 - 1.5 Hz, respectively. The high frequency bandpass produces signals which are about twice as large as the low frequency bandpass. Therefore the second trace was multiplied by 1.5 to counteract large amplitude differences between the waveforms. Finally, the resulting traces were added after shifting the low frequency trace by 0.2 s and without shifting the traces to obtain the pilot and its closely similar waveform. This procedure mimics the generation of composite signals due to multipathing. In other words the obtained signals consist of two or more distinct signals which arrive with different slowness and amplitude values at about the same time at slightly different station locations. The length of the pilot (solid line) is chosen to be 1.8 s and is marked by the vertical bars in Figures a and b. Figure b shows 10 examples of waveform pairs which are generated by the described procedure. The numbers at the upper left and right mark the lag times which correspond to the best waveform fit using CCGN and PCC, respectively. 5000 waveform pairs have been generated and correlated. The lag time distributions of the best waveform fits are presented in Figures c (PCC) and d (CCGN). The histograms in the dark grey tones show the distribution of the 2500 best correlations.

It can be seen that the distributions are significantly different. The PCC lag time distribution shows a balanced waveform alignment between both signals, i.e. at -0.2 s and 0 s lag time. Conversely, the CCGN lag time distribution contains a clear maximum at 0 s. This means that the waveform alignment is governed by the high frequency signal (a(t) in Figure a) which has not been shifted in time prior to summation. On average this signal is larger than the low frequency signal and consequently favored by the CCGN-measure. A considerable amount of waveform pairs have been aligned with positive lag times (maximum at about 0.25 s). In these cases the coherence measures advocate a negative waveform correlation. If PCC is used then these cycle skips will rapidly decrease with increasing pilot lengths. For instance, increasing the length by 0.5 s decreases the number of cycle skips to about one fifth for PCC while the number of cycle skips of the CCGN-measure remains almost unchanged. The CCGN lag time distribution shows only minor changes while the PCC lag time distribution contains an increased number of correctly aligned waveforms. The example from the Figure  shows the ability of PCC to detect coherent weak amplitude features which are concealed by larger amplitude signals.
 

Following figure is only to show the different sensitivity of both measures:

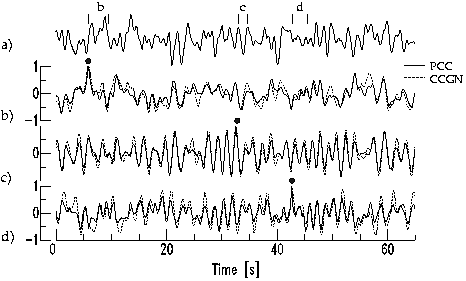a) Seismic test trace and three pilot wavelets used to calculate the PCC's and the CCGN's which are shown in figures b-d. The vertical lines mark the begin and end times of the employed pilots. We use the labels b,c, and d to refer to these wavelets. b) PCC (solid line) and CCGN (dotted line) between wavelet b and test trace. c) Same as b) but wavelet c is used. d) Same as b) but wavelet d is used.

Figure a shows a random time-series and three arbitrarily selected pilots. We label these wavelets b, c, and d. Their begin and end times are marked by the vertical lines. Wavelet b and d look complicated and are distinct from the rest of the trace. Conversely wavelet c is not recognizably different from other portions of the time-series. Figures b, c, d show the PCC's (solid lines) and CCGN's (dashed lines) between the wavelets b, c, d  and the trace from Figure a. The black dots mark the absolute maxima of the cross-correlograms which are located at the beginning of the pilot wavelets. They mark what we call signal in this example. As can been seen in the Figure, the signal-to-noise ratio (S/N) of the different cross-correlograms depends on the waveform complexity of the pilot waveform. Note that the S/N ratio is large whenever a distinct waveform (Figures b, d) is used for the correlation. Conversely, the S/N ratio is small for the cross-correlation with wavelet c (Figure c). This is expected and caused by the large resemblance of the wavelet c with the waveforms in the rest of the trace. Note also that the qualitative comparison of the cross-correlograms (PCC and CCGN) shows the ability of PCC to further increase the S/N ratio. The ratios of the root-mean-square (rms) amplitudes CCGN-to-PCC are 1.28, 1.25, and 1.58 for the traces from Figures b,c, and d. This can be interpreted as a stronger sensitivity of waveform similarity in the PCC measure.